A Mandelbrot set visualization on the iPhone
A colleague of mind was reading a book about Mandelbrot lately and that reminded me of a coursework I was given at UCL in my introductory course to Java. The purpose was to draw a visualization of the Mandelbrot set in Java. I looked back through my university folder on my Mac to find the coursework. Well, my first impression was: you can write pretty ugly code while a student ;).
But then while reading through my code I thought it would be quite funny to try to re-implement that on the iPhone. Obviously, given the dozens of fractal apps already available on the App Store this would never become an app but it was a funny one so I gave it a go.
In a nutshell, the Mandelbrot set is a mathematical set of points in the complex plane (the complex plane being a geometric representation of complex numbers on a real and imaginary axis). A complex number c belongs to the Mandelbrot set if the orbit of 0 under iteration of the complex quadratic iteration $Z_{n+1} = Z_{n}^{2} + c$ remains bounded. So assuming we have a complex number c with real part x and imaginary part y such that $c = x + iy$, we can conclude that it belongs to the Mandelbrot set if given the following iteration: $$Z_{0} = c$$ $$Z_{n+1} = Z_{n}^{2} + c$$ Z never escapes to infinity. It has been shown that if the magnitude of Z ever becomes greater than 2, it will eventually escapes to infinity. We thus simply have to compute the magnitude of Z for a large number of iterations and check whether it goes beyond 2 to conclude it does not belong to the set. Before going any further, we have to define two properties of complex numbers: how to multiply two complex numbers and how to compute the magnitude of a complex number. Assuming we have two complex numbers defined by $$c_{1} = a + ib$$ $$c_{2} = c + id$$ their product is then given by $$c_{1}c_{2} = (ac-bd) + (bc+ad)i$$
Thus taking the square of $c_{1}$ would result in $$c_{1}^{2} = (a^{2}-b^{2}) + 2abi$$
The magnitude (or absolute value) of a complex number c is defined as $$|c| = \sqrt{a^{2}+b^{2}}$$
Given these 2 definitions, we now simply have to check whether the magnitude for each step of the complex quadratic iteration exceeds 2 (to avoid computing a square root, we can simply check whether the sum of the squares of both real and imaginary parts exceeds 4).
The C function written to check that is the following
BOOL isInMandelbrotSet(float re, float im)
{
float x = 0 ; float nx ;
float y = 0 ; float ny ;
bool fl = TRUE ;
for(int i = 0 ; i < MANDELBROT_STEPS ; i++)
{
// We calculate the real part of the sequence
nx = x*x - y*y + re ;
// We calculate the imaginary part of the sequence
ny = 2*x*y + im ;
// We compute the magnitude at each step
// We check if it's greater than 2
if((nx*nx + ny*ny) > 4)
{
fl = FALSE ;
break ;
}
x = nx ;
y = ny ;
}
return fl ;
}
The number of steps is arbitrary but we can obtain accurate results by only taking 50 steps.
We then have to compute the previous check for each pixel on the frame. In order to get faster computation, I decided to create a bitmap context, draw the Mandelbrot set offscreen and simply create an image from the bitmap context and draw it to the current context in the drawRect: method.
We first need to create a bitmap context by calling the following method
- (CGContextRef)createCustomBitmapContextWithSize:(CGSize)size
{
CGContextRef context = NULL ;
int bitmapBytesPerRow = (size.width * 4) ;
bitmapBytesPerRow += (16 - bitmapBytesPerRow%16)%16 ;
size_t bitmapByteCount = (bitmapBytesPerRow * size.height) ;
CGColorSpaceRef colorSpace = CGColorSpaceCreateDeviceRGB() ;
void *bitmapData = malloc(bitmapByteCount) ;
if (bitmapData == NULL)
{
fprintf (stderr, "Memory not allocated!") ;
return NULL ;
}
context = CGBitmapContextCreate(bitmapData, size.width, size.height, 8, bitmapBytesPerRow, colorSpace, kCGImageAlphaPremultipliedLast) ;
if (context == NULL)
{
free (bitmapData) ;
bitmapData = NULL ;
fprintf (stderr, "Context not created!") ;
return NULL ;
}
CGColorSpaceRelease(colorSpace) ;
return context ;
}
The drawing method is then given by the following
- (void)drawMandelbrot:(CGPoint)center andZoom:(CGFloat)zoom
{
CGContextSetAllowsAntialiasing(bitmapContext, FALSE) ;
CGContextSetRGBFillColor(bitmapContext, 0.0f, 0.0f, 0.0f, 1.0f) ;
CGFloat re ;
CGFloat im ;
// mapping the bounding box to pixels
/*
zoom 1 has to be between -2 to 1 and -1 to 1
any additional zoom divides these by the zoom
*/
// loop through every pixel of the frame...
for (int i = 0 ; i < 480 ; i++)
{
for (int j = 0 ; j < 320 ; j++)
{
re = (((CGFloat)i - 1.33f * center.x)/160) ; // -2 to 1 - screen width = 480
im = (((CGFloat)j - 1.00f * center.y)/160) ; // -1 to 1 - screen height = 320
re /= zoom ;
im /= zoom ;
if (isInMandelbrotSet(re, im))
{
CGContextFillRect (bitmapContext, CGRectMake(i, j, 1.0f, 1.0f)) ;
}
}
}
}
I did not have time (or interest..) for implementing various zoom level so we simply draw at the most basic zoom (in the bounding box -2 to 1 on the real axis and -1 to 1 on the imaginary axis).
The result is quite nice. Again, I did not have much time to implement different colors but it should be trivial to add this feature (the color basically depends on how many steps it takes for the magnitude of Z in the iteration to exceed 2).
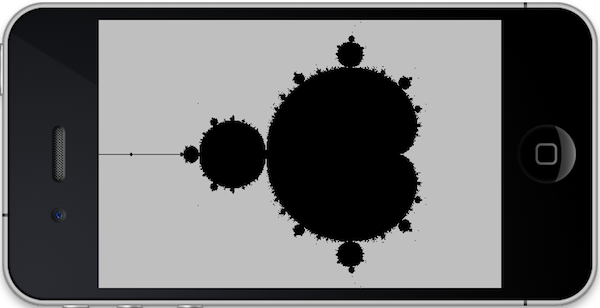
By running the drawing code on my iPhone 4 with 50 Mandelbrot steps per pixel, I achieve the following timing (in seconds):
- bitmap context creation duration = 0.105825
- drawing Mandelbrot in bitmap duration = 0.684840
- draw rect duration = 0.107269
This could obviously be improved but for the purpose of the experiment (fun!) I'm quite happy with it!
I have uploaded the project to GitHub so give it a go and have fun ;).