Sorting algorithms comparison
I have been working on sorting algorithms during the last week and I thought it would be worth writing a small article about it. Trying to sort an array "brute-force" in any programming language would almost always take ages and could lead to memory overflows. Fortunately, many efficient sorting algorithms have been designed. However, not every algorithm is as efficient and each algorithm performs better or worse in some given situations. As a starting point, let's first illustrate the complexity of five famous algorithms (I am not a big fan of Bubble Sort but it's also worth to show bad examples in order to fully illustrate a topic):
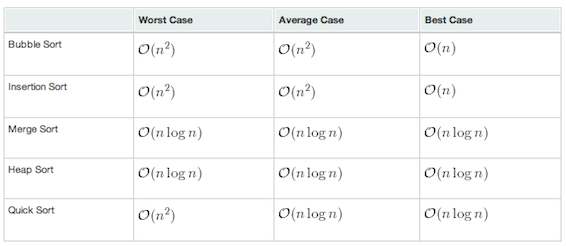
Furthermore, in order to illustrate better the overall complexity of each algorithm, let's look at the running time of each algorithm for various array sizes in three very different situations:
- when the array is already sorted (which leads to best case scenario for some algorithms but as we will see, not all of them).
- when the array is already sorted but in reverse order (leads to worst case scenario for simple algorithms).
- when the array is randomly ordered.
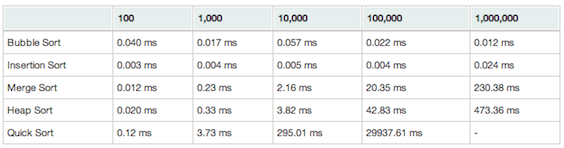
Sorted array:
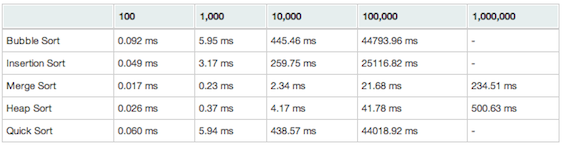
Reverse sorted array:
Randomly sorted array:
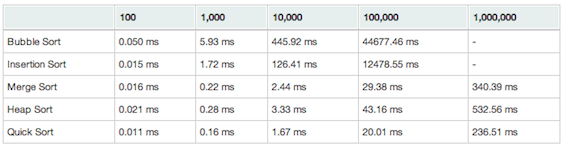
We randomly sorted the array by generating its elements with the following routine:
int arraySize = 10000 ;
int array[arraySize] ;
srandom(time(NULL)) ;
for (int i = 0 ; i < size ; i++)
array[i] = random() % size ;
(Note that '-' simply means that I did not have the patience to wait for the algorithm to return... You get the idea anyway).
The first comment we can make out of this data is that Merge Sort performs indeed quite well on average and does not give bad results even in the worst case. However, for each situation it is outperformed by another algorithm, Bubble and Insertion Sorts when the array is already sorted and Quick Sort when the array is randomly sorted. The reason is that when the array is already sorted, simple algorithms such as Bubble Sort and Insertion Sort reach their best case scenario (but reaching their worst case scenario if the array is sorted in reverse order). Furthermore, even if Quick Sort and Merge Sort have same complexity on average and in best case scenario, the constants (hidden by the big-O notation) are much smaller in Quick Sort leading to a smaller running time on average. However, the pitfall is that Quick Sort performs bad in the worst case scenario so it can be quite of a risky alternative.
So, even if we can consider Merge Sort a "safe alternative" that guarantee good results in any case, it is very often simply not the best option. The reason is mainly that the worst-case scenario is after all really rare and believe it or not, half of the time you try to sort an array, it is actually already sorted. In that case, Merge Sort will still perform in $\mathcal{O}(n\log{n})$ while Insertion Sort for instance will perform in $\mathcal{O}(n)$.
So my piece of advice is:
- analyse the problem carefully before deciding the sorting algorithm.
- often, for small arrays or arrays that are already (or almost) sorted, Insertion Sorting will do the job and even perform better than a more complex algorithm.
- if you care about memory, avoid Merge Sort since it basically uses loads of temporary arrays that will easily overflow your memory.
- even if Quick Sort has a $\mathcal{O}(n^{2})$ worst case, remember that worst case is often rare and Quick Sort will perform much better that Merge Sort on average since its constants (hidden by the big-O notation) are actually much smaller.
Following is a C implementation of the five algorithms.
Bubble sort
void bubbleSort(int array[], int min, int max)
{
// loop through every item in the array
for (int i = min ; i <= max ; i++)
{
// loop a second time from the back of the array
for (int j = max ; j > i ; j--)
{
// swap the elements if necessary
if (array[j-1] > array[j])
{
int copy = array[j-1] ;
array[j-1] = array[j] ;
array[j] = copy ;
}
}
}
}
Insertion sort
void insertionSort(int array[], int min, int max)
{
int key ;
// we loop through all elements in the original array from the second element
for (int j = 1 ; j <= max ; j++)
{
// store the current element as the key
key = array[j] ;
// get the element just before the current element
int i = j - 1 ;
// loop through all elements from the key to the start
// check if the current element is smaller than the key
while (i >= 0 && array[i] > key)
{
// we move the current element backward
array[i+1] = array[i] ;
i-- ;
}
// we finally move the key
array[i+1] = key ;
}
}
Merge sort
void mergeSort(int array[], int min, int max)
{
// prerequisite
if (min < max)
{
// get the middle point
int mid = (int)floor((max+min)/2) ;
// apply merge sort to both parts of this
mergeSort(array, min, mid) ;
mergeSort(array, mid+1, max) ;
// and finally merge all that sorted stuff
merge(array, min, max, mid) ;
}
}
void merge(int array[], int min, int max, int mid)
{
int firstIndex = min ;
int secondIndex = mid + 1 ;
int index = min ;
int tempArray[max] ;
// if there are still objects in both arrays
while ((firstIndex <= mid) && (secondIndex <= max))
{
if (array[firstIndex] < array[secondIndex])
{
tempArray[index] = array[firstIndex] ;
index++ ;
firstIndex++ ;
}
else
{
tempArray[index] = array[secondIndex] ;
index++ ;
secondIndex++ ;
}
}
// terminates the object of the lower array
while (firstIndex <= mid)
{
tempArray[index] = array[firstIndex] ;
index++ ;
firstIndex++ ;
}
// terminates the object of the upper array
while (secondIndex <= max)
{
tempArray[index] = array[secondIndex] ;
index++ ;
secondIndex++ ;
}
// transfer to the initial array
for (int i = min ; i < index ; i++)
array[i] = tempArray[i] ;
}
Heap sort
// returns the left node (by doubling the current node)
int leftNode(int node)
{
return node << 1 ; // this actually does 2*node
}
// returns the right node (by doubline the current node and adding 1)
int rightNode(int node)
{
return (node << 1) + 1 ; // this actually does 2*node+1
}
// return the parent node (by taking the half of the
// current node and returning its floor)
int parentNode(int node)
{
return (int)floor(node/2) ;
}
// restore the heap property
void maxHeapify(int array[], int i, int heapSize)
{
// get the two children nodes
int left = leftNode(i) ;
int right = rightNode(i) ;
// assume that the largest is originally the current node
int largest = i ;
// check if the left node is the largest
if (left <= heapSize && array[left] > array[i])
largest = left ;
// check if the right node is the largest
if (right <= heapSize && array[right] > array[largest])
largest = right ;
// in case the left or right node was larger than the parent
if (largest != i)
{
// we switch the parent with the largest child
int temp = array[i] ;
array[i] = array[largest] ;
array[largest] = temp ;
// and apply maxHeapify recursively to the subtree
maxHeapify(array, largest, heapSize) ;
}
}
// build the heap by looping through the array
void buildMaxHeap(int array[], int heapSize)
{
for (int i = (int)floor(heapSize/2) ; i >= 0 ; i--)
maxHeapify(array, i, heapSize) ;
}
void heapSort(int array[], int arraySize)
{
// determine the heap size
int heapSize = arraySize ;
// build the heap
buildMaxHeap(array, heapSize) ;
// loop through the heap
for (int i = heapSize ; i > 0 ; i--)
{
// swap the root of the heap with the last element of the heap
int temp = array[0] ;
array[0] = array[i] ;
array[i] = temp ;
// decrease the size of the heap by one so that the previous
// max value will stay in its proper placement
heapSize-- ;
// put the heap back in max-heap order
maxHeapify(array, 0, heapSize) ;
}
}
Quicksort
int partition(int array[], int min, int max)
{
// define a pivot as the max item of the (sub)array
int pivot = array[max] ;
int i = min - 1 ;
// loop through the elements of the (sub)array
for (int j = min ; j < max ; j++)
{
// in case the element has a smaller value that the pivot
// bring it in front of it (larger elements will come after it)
if (array[j] <= pivot)
{
i++ ;
int temp = array[i] ;
array[i] = array[j] ;
array[j] = temp ;
}
}
// bring the pivot to its correct position
int temp = array[i+1] ;
array[i+1] = array[max] ;
array[max] = temp ;
return i+1 ;
}
void quickSort(int array[], int min, int max)
{
if (min < max)
{
// partition the array in two parts
int q = partition(array, min, max) ;
// apply QuickSort recursively to both parts
quickSort(array, min, q-1) ;
quickSort(array, q+1, max) ;
}
}